§49. Закон генетического равновесия Харди – Вайнберга
Цель изучения этой темы: объяснить закон генетического равновесия Харди – Вайнберга.
Что такое популяция? Чем она отличается от вида? Каков главный признак этого понятия? Что такое рецессивная аллель, доминантная аллель, генотип, фенотип, полное и неполное доминирование?

Что нужно повторить для успешного изучения темы? § 33 и 60 – учебник для 9 класса.
Формулирование популяционной генетики. Как вы помните, популяция – это группа особей одного вида, длительно живущая на определенной территории, постоянно свободно скрещивающаяся (не менее 100 поколений подряд) и имеющая общий генофонд. Популяции изменчивы. Они могут погибать, распадаться, мигрируя или увеличивая свою численность, смешиваться с другими популяциями и т. д. С начала ХХ в. ученые пытались изучать генетику популяции. Так изучением реальных природных популяций занимался С. С. Четвериков, открывший явление популяционных волн и признанный основателем популяционной генетики. Одним из крупнейших открытий в этой области считается закон генетического равновесия Харди – Вайнберга. Его математическим выражением является формула, позволяющая рассчитать соотношение генотипов в идеальной популяции. Почему же популяция должна обязательно быть идеальной? Да просто потому, что множество влияющих факторов вносят разные коррективы в реальную жизнь. Это не значит, что данная формула вообще не годится для расчета генотипов в реальных популяциях. Совсем нет. Если популяция находится в равновесии, она стабильна, то вполне возможно, что она будет полностью отвечать требованиям идеальной популяции. Рассмотрим подробнее саму формулу, или уравнение.
Уравнение Харди – Вайнберга исходит из того, что по определенному гену существуют две аллели – доминантная А и рецессивная а. Соответственно, все особи популяции должны обладать какими-то из этих аллелей, в каких-то определенных соотношениях. Но так как аллелей две, только они будут у всех особей популяции. Следовательно, верна будет формула: А+а=1 (или 100%), это не вызывает сомнений. Для формулы авторы решили обозначить аллели иными символами. Для А – p, а для а – q. Теперь формула приобретает вид: p + q = 1 (или 100%). Это соотношение аллелей, а формула позволяет рассчитать соотношение генотипов. Вспомним, что для моногибридного скрещивания, в котором существуют всего две аллели – доминантная и рецессивная, возможно только три вида генотипов. Это доминантная гомозигота АА, гетерозигота Аа и рецессивная гомозигота аа. В результате формула соотношения генотипов выглядит следующим образом: p² + 2pq + q² = 1 (или 100%). Или, если обозначить генотипы классическими символами, то вид уравнения будет следующий: А² + 2Аа + а² = 1 (или 100%).
Решение уравнения Харди – Вайнберга. Есть стандартный набор действий, позволяющий решить данное уравнение, если нам известна одна из величин. В курсе алгебры 8 класса вы ознакомились с ними. Для желающих в этом параграфе мы даем подробную пошаговую инструкцию, по которой удобно решать данное уравнение.
Итак, поговорим об условии задачи, решаемой с помощью формулы Харди – Вайнберга. Предположим, в некоем заповеднике средней площади, но четко ограниченном от окружающих его незаповедных территорий, проживает популяция зайцев, хорошо описанная учеными-экологами, благодаря скрытым камерам, фотоловушкам и систематическим наблюдениям. Точно известно, что количество особей в этой заповедной популяции – 3728. Из них светло-серой окраской обладают 849 особей. Исходя из количественных соотношений, логично предположить, что именно светло-серая окраска является рецессивной, а темно-серая – доминантной. Следовательно, особей с генотипом аа – 849. Нам необходимо найти общее количество гетерозигот и доминантных гомозигот. Ход решения следующий:
1) Чтобы выяснить значение q², необходимо разделить количество рецессивных гомозигот – 849 на общее число особей популяции – 3728, так как все особи популяции и составляют 100%, или 1. Следовательно:
q²= 849 : 3728 = 0,2277.
2) Чтобы узнать значение q, имея значение q², необходимо извлечь корень. Извлекаем корень из 0,2277 = 0,477. Следовательно, q = 0,477.
3) Чтобы узнать значение p, отнимаем q от 1. Вычитаем 1 – 0,477 = 0,523. Следовательно, p = 0,523.
4) Чтобы узнать значение 2pq, перемножаем их значения и умножаем на 2: 0,477 × 0,523 × 2 = 0,499. Следовательно, 2pq = 0,499.
5) Чтобы получить количество гетерозигот в процентах, умножаем 0,499 на 100%. Получаем 4,99 или цифру, близкую к 5%.
6) Чтобы узнать абсолютное количество гетерозигот – носителей рецессивной аллели серой окраски, имеющих темно-серый доминантный фенотип из общего количества особей в популяции, проведем вычисление через пропорцию: 5%×3728/100%=186 гетерозигот Аа.
7) Проверим выполненные расчеты, высчитав количество доминантных гомозигот АА тем же способом. Если p = 0,523, следовательно:
p² = 0,523 × 0,523 = 0,273.
Исходя из формулы p² + 2pq + q2 = 1, подставляем имеющиеся значения:
0,273 + 0,499 + 0,2277 = 0,9997.
Если округлить, ответ равен 1. Почему возникла цифра на десятитысячные меньше единицы? Это произошло потому, что уже в первом действии мы округлили величины до четвертого знака после запятой.
Условия идеальной популяции. Как уже говорилось ранее, уравнение Харди – Вайнберга соблюдается не в любой природной популяции. Рассмотрим, какие же условия должны выполняться, чтобы популяция находилась в равновесии и к ней было применимо данное уравнение.
1) Популяция должна быть свободно скрещивающейся, а негермафродитной, несамоопыляемой и неклонирующейся. Значит, например, для гаплоидных дрожжевых грибков данная формула, конечно, не подойдет.
2) В популяции не должно быть мутационного процесса и не должны появляться новые аллели. Ведь они в формуле не учитываются.
3) В популяции не должно быть значительных миграций. Иными словами, не должно быть такого, чтобы, например, большая часть светло-серых зайцев убежала в соседний лес, а оттуда прибежали темно-серые зайцы и т. д. Если происходит катаклизм, например лесной пожар, то число «мигрантов» может превосходить всю исходную популяцию. Понятно, что в таких условиях никакие формулы не будут отражать реальную картину распределения количественного соотношения аллелей. Ведь тогда это будет уже «новая популяция», которую снова надо исследовать, подсчитав зайцев разных окрасок и произведя вычисления.
4) Против одной из аллелей не должен действовать естественный отбор. Если носители определенной аллели будут все время погибать или оставаться бесплодными, то уравнение тоже не будет «работать». Ведь предполагается, что генотипы примерно равны по степени выживаемости их носителей, а аллели равны по вероятности перейти к потомкам.
5) Популяция не должна быть очень малочисленной. Ведь в малочисленных популяциях может легко погибнуть значительная часть особей (более 50%), а случайно выживут представители с каким-то одним генотипом. Кроме того, в малочисленных популяциях происходят близкородственные скрещивания, что в принципе повышает гомозиготность и делает их генетически нестабильными.
Идеальная популяция, генетическое равновесие, доминантный, рецессивный, гомозигота, гетерозигота, дрейф генов.

Знание и понимание
1. Как вы понимаете, что такое популяция и ее генофонд?
2. Определите связь между буквенными символами А, а, p, q, А², 2Аа, а², p², 2pq, q² и генетическими терминами: рецессивная аллель, доминантная аллель, рецессивная гомозигота, доминантная гомозигота, гетерозигота. Какие из них каким соответствуют?
Применение
1. Для чего применяют уравнение Харди – Вайнберга?
2. Назовите, при каких условиях в природной популяции может не соблюдаться уравнение Харди – Вайнберга?
Анализ
1. Изобразите в виде схемы условия, которым должна соответствовать идеальная популяция, чтобы в ней полностью соблюдалось равновесие Харди – Вайнберга.
2. Докажите на примерах, что, зная количество рецессивных гомозигот, можно высчитать количество всех носителей рецессивной аллели в популяции.
Синтез
1. Порассуждайте, почему при малом количестве особей в изолированной популяции перестает действовать закон генетического равновесия Харди – Вайнберга, но начинает действовать явление дрейф генов.
2. Порассуждайте и обоснованно докажите, для каких из перечисленных популяций точно не будет действовать закон генетического равновесия Харди – Вайнберга, а для каких будет действовать с большой долей вероятности. Объясните, почему.
1) Среди 100 000 клеток стафилококковой инфекции обладают резистентностью к антибиотику 68.
2) На поле гороха посевного среди 7589 горошин найдено 1392 зеленых, остальные желтые.
3) На приусадебном участке, где выращивается капуста, в июне обнаружено 1256 тлей, из них 390 – пестро-серые, остальные имеют сплошную зеленоватую окраску.
4) На поле поймано 4711 кузнечиков, 482 из которых были желтые, остальные зеленые.
5) Больные сахарным диабетом встречаются с частотой 1 из 200.
6) Находящийся на горной вершине Тибета эндемичный вид саранчи насчитывает 429 особей, из них 33 обладают недоразвитыми крыльями, а остальные нормальными.
7) На территории заповедника экологами отслежено 2376 волков, из которых 98 – коротконогие, остальные имеют нормальную длину ног.
Оценка
1. Напишите реферат об истории открытия и применении закона генетического равновесия Харди – Вайнберга.
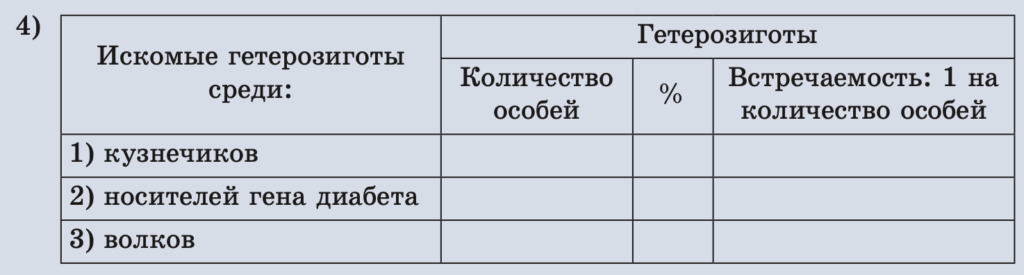
2. Оцените количество гетерозигот в следующих случаях и показателях:
1) На поле поймано 4711 кузнечиков, 482 из которых были желтые, остальные зеленые.
2) Больные сахарным диабетом встречаются с частотой 1 из 200 среди 18 млн населения. Каково количество носителей данной болезни?
3) На территории заповедника экологами отслежено 2376 волков, из которых 1978 – коротконогие, остальные имеют нормальную длину ног.